题目 63.不同路径-ii
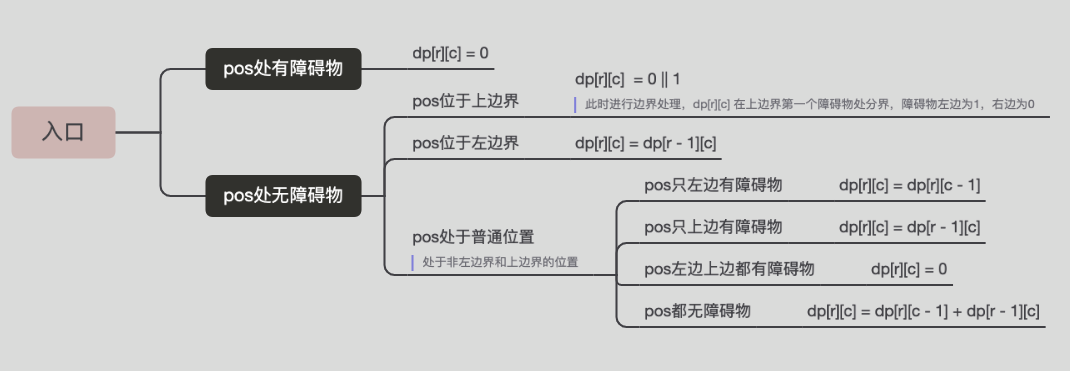
分析 此题在未进行空间优化使用二维数组的方案时,可以很好地解决边界问题。
pos 处有障碍物
pos 处在上边界(r == 0)
pos 处在左边界(c == 0)
其他普通情况
1 : pos只左边有障碍物 dp[r][c] = dp[r][c - 1 ]2 : pos只上边有障碍物 dp[r][c] = dp[r - 1 ][c]3 : pos左边上边都有障碍物 dp[r][c] = 0 4 : pos都无障碍物 dp[r][c] = dp[r][c - 1 ] + dp[r - 1 ][c]
上述分析可以得到一个初步的代码版本
class Solution : def uniquePathsWithObstacles (self, obstacleGrid: List[List[int]]) -> int: columnLen = len(obstacleGrid[0 ]) rowLen = len(obstacleGrid) note = [0 ] * columnLen for i,v in enumerate(obstacleGrid[0 ]): if v == 1 : break note[i] = 1 if rowLen == 1 : return note[-1 ] ret = 0 for r in range(1 , rowLen): for c in range(columnLen): if obstacleGrid[r][c] == 1 : ret = 0 note[c] = 0 continue if c == 0 : ret = note[c] continue if obstacleGrid[r - 1 ][c] == 1 : if obstacleGrid[r][c - 1 ] == 1 : ret = 0 note[c] = 0 else : note[c] = ret else : if obstacleGrid[r][c - 1 ] == 1 : ret = note[c] else : ret = ret + note[c] note[c] = ret return ret
普通情况可进行合并
普通情况合并 1 : pos只左边有障碍物 dp[r - 1 ][c] = 0 , dp[r][c] = dp[r][c - 1 ] + dp[r - 1 ][c]2 : pos只上边有障碍物 dp[r][c - 1 ] = 0 , dp[r][c] = dp[r][c - 1 ] + dp[r - 1 ][c]3 : pos左边上边都有障碍物 dp[r - 1 ][c] = 0 , dp[r][c - 1 ] = 0 , dp[r][c] = dp[r][c - 1 ] + dp[r - 1 ][c]4 : pos都无障碍物 dp[r][c] = dp[r][c - 1 ] + dp[r - 1 ][c]
即普通情况下
dp[r][c] = dp[r][c - 1 ] + dp[r - 1 ][c]
class Solution : def uniquePathsWithObstacles (self, obstacleGrid: List[List[int]]) -> int: columnLen = len(obstacleGrid[0 ]) rowLen = len(obstacleGrid) note = [0 ] * columnLen ret = 0 for i,v in enumerate(obstacleGrid[0 ]): if v == 1 : break note[i] = 1 if rowLen == 1 : return note[-1 ] for r in range(1 , rowLen): for c in range(columnLen): if obstacleGrid[r][c] == 1 : ret = 0 note[c] = 0 continue if c == 0 : ret = note[c] continue ret = ret + note[c] note[c] = ret return ret
BMW WARNING 本文首发于 skyline.show 欢迎访问,Github仓库 点亮⭐️。
I am a bucolic migant worker but I never walk backwards.
参考资料如下列出,部分引用可能遗漏或不可考,侵删。
63.不同路径-ii
本文作者: Skyline(lty)
文章链接:http://www.skyline.show/力扣题解 63-不同路径-ii.html
授权声明: 本博客所有文章除特别声明外, 均采用 CC BY - NC - SA 3.0 协议。 转载请注明出处!
如果觉得我的文章对您有用,请随意打赏。您的支持将鼓励我继续创作!